My data lab

1.Related work

Mobilenet V2 - Related work

Develop of NN architecture

-model design

-hyperparameter optimization

-network pruning

-connectiviy learning(?) > shufflenet (?)

-genetic algorithms to optimizer

-reinforcement learning to architectural search

>> too complex

2. Architecture Strategy

a.  우린 각각의 NN 의 각 layer가 manifold of interest 를 form 한다고 알고있습니다. (명확하진 않지만 통속적으로)

b.  그 때 manifold of interest 는 더 적은 차원의 subspace 에 embedding 될 수 있다고 오랫동안 가정해왔습니다.

c.  CNN 에서 독립적인 d개의 체널 pixel 을 보면 information 이 이 곳에 Some manifolod를 형성하며 encoded 되어 있습니다.

d. mobilenet v1 에서도 보앗듯이 width multiplyer  manifold of interest 가 dense 하게 span 할 때까지 dimensinality 를 감소시킵니다.

e. 하지만 이것은 NN 이 non-linear transformation 을 포함할 때 깨지게 됩니다. ( 이 논문에서 실험하였음)

f.  Relu 를 예를 들자면, 아래와 같이 Relu 의 output 형태를 보면 1차원이기 때문에  output space 를 보면 , piecewise linear curve 를 형성합니다.

f -2 . 이것을 다르게 해석하면 Deep network 는 최종 output activation 에 의해  오직 1차원적인 classifier 로서 동작하게됩니다. 이때 output domain 에서 생각해보면 non-zero volume (finte?) 을 형성하게됩니다.

g. 우리는 추가적으로 input manifold 가 low-dimensional subspace 에 embedding 될 수 있다면,  Relu transformation 이

그 information 을 preserve 하는 것을 증명하였습니다.  필요조건이 있는데[그것의 복잡도를 포함하기 위한 set of expressible functions 찾을 수 있다면

이어서 이 정리에 대한 내용만 설명해보자면

S 는 compact, fB = Relu(BX) : Rn => Rm, P(B) = pdf on Matrix 

>> 결론,  fb 로 부터 유도(collapse~축소)된 m 차원공간 space 의 average n-volume 은, 

V - (Nm,n)/ (2^m) V = V(1-(Nm,n)/ (2^m)) = Vol(S) * 0.xxx 즉  처음 정의한 S 라는 compact 공간에 Embedding 된다.

#summary for bottleneck

1. If the manifold of interest remains non-zero volume after ReLU transformation, it corresponds to a linear transformation.

2. ReLU is capable of preserving complete information about the input manifold, but only if the input manifold lies in a low-dimensional subspace of the input space.

(3). Experimental evidence suggests that using linear layers is crucial as it prevents nonlinearities from destroying too much information

1.  manifold of interest 가 RELU이후 non zero volume 을 남긴다면, 이것은 linear transform에 대응됨

2. RELU 는 information 을 preserve 할 수 있는 가능성이있다, 하지만 오직 input manifold 가 low -dimensinal subspace 의 lie 될 때만

3. Exprimental 이 증명한다, Linear layer 이 information 이 destroy 되는 것을 막아준다고. 

ex

>Bottleneck 은 일종의 최적으로 압축된  Manifold 로 Encoding 된 정보의 집합

ex)CNN , Image recognition 은 2번가정에 매우 적합할 수 밖에 없다.

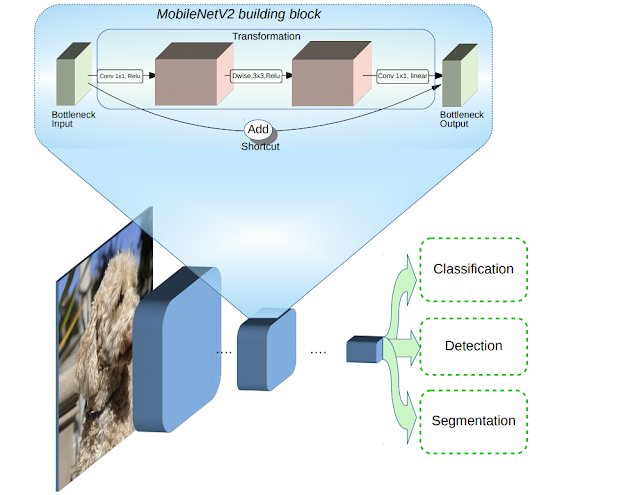
#Inverted Residuals

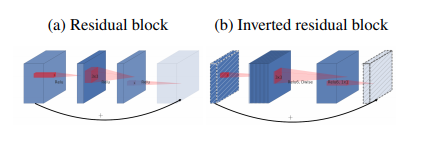
기존에 있던 Residual bolck 을 반대로 하는것이다.

Residual 에 대해서 먼저 이야기 하자면, Residual 이 사용되는 가장 큰이유는 앞서말한 정보 파괴를 막기 위해 Residual 을 만들어 주게 된다.

하지만 이논문에서는 이것을 반대로 뒤집어서 하게되는데,

첫번째 가정이 inverted residual  block 을 돌리기 이전에 이미 bottleneck 을 만든다는 것이다.

 이미 축소된 subspace 로 embedding 시키고 그것을 residual 하게되면 메모리, 연산량 측면에서 많은 이점을 갖게된다.

왜 굳이 conv 할때 expand 하는지에 대해서 묻는다면?

이 channel expand 의 역할은 비선형을 포함 할 수 있도록 도와주는 Detail 의 역할을 한다고한다.

결론적으로 채널수 / memory 수를 비교해보면 더  bottleneck 을 만들어 놨다는 것을 알 수 있다.

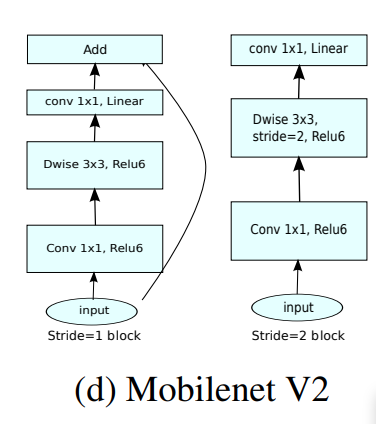
이것을 보면 Stride 가 1/2 일 때  block 이 상이 한데,

Stride 2 는 Residual 이 없는 것을 확인 할 수 있다.

그 말인 즉슨,  Resolution 자체가 줄어들 때는, 체널을 넓늘려가며 충분히 information을 담는 parameter 자체는 늘어나도록 

신경을 썻고, Stride 1  ,Resolution 자체가 유지될 때는, Inverted Residual 을 넣어 원래 정보를 유지시키는 대 집중 하고, 그안에서 더 높은차원의 data 를 expand and squeeze 를 사용해서 추출해서 detail 로 사용 했다고 보면 된다. 

Q 64 >96 160 >320 의 역할은 무엇일까. 오히려 체널을 bottleneck 을 했다가 다시 넓히는 이유가 있을까?

결론 : impressive as our ecg signal