ref : Hierarchical Latent Vector Model for learning Long-terim Strucutre in Music
오늘 리뷰할 논문은 LSTM 구조를 VAE 로 활용해서 Music data Reconstruction 을 시도한 논문을 설명하겠습니다.
2.Back ground
2-1.Recap VAE


VAE 에대해서 잘 설명해 놓은 그림이다.
기존 AutoEncoder 는 Encoder 와 Decorder 로 이루어져있는데 잠재공간에 대해서 별다른 제약을 두지 않는다.
VAE 는 잠재공간을 가우시안 분포들로 latent space 를 이룰 것이라 가정하고 출발한다.
VQ-VAE, Diffusion 모델도 이와 비슷한 가정으로 출발 하는 것으로 생각하고있다.
VAE는 AE 처럼 직접적으로 latent space 를 맵핑하는 대신, 평균(뮤) 과 분산(시그마) 를 이용해 latent space 를 맵핑하려고합니다. 결과적으로 2번째 scatter plotting 된 것 과 같이, VAE 에서 맵핑된 latent 를 plotting 하면 가우시안(구형분포) 를 가지는 것을 볼 수 있다.

다시 첫번째 그림+수식으로 설명하자면
VAE의 목적은 Generative model 을 만드는 것인데, 일단 쉽게 생각해보면 이미지 Reconstruction 하는 것과 유사합니다.
Generative model 은 결국 P(x) 를 1로 만들자(확률분포의 총합은 1), 즉 생성된 데이타 x 의 확률분포가 원래의 x 와 같게 나올 확률을 높게 만드는 것이기 때문에 결국 log p(x) 를 크게 만들면 되는 것입니다.
왼쪽에 식은 VAE 의 구조를 이용해서 유도되는 log p(x) 의 하한 선인데,
VAE = q_lambda(z|x) (Encoder) * p_seta(x) (Decoder) 로 전개 할 수 있는데
p_seta(x) Basyian rule 을 사용하게되면 eq 1 부등식이 나오게된다.(참고:https://process-mining.tistory.com/161)
우리의 목적은 우항을 크게만드는건데 왼쪽항이 lowerbound 역할을 하기때문에 Evidence Lower bound, ELBO 라고한다.(왜굳이 이런 내용을 줄여서말하는지-_-ㅋ)
Eq1 에서 좌항은 loss 로 만들기 좋다, 왜냐하면 왼쪽항은 Decoder 를 통해서 나오는 x 의 Reconstruction loss 이며
두번째 Term 인 KL divergence 는 Encoding 되어 만들어진 z와 원래 z 분포의 KL divergence term 이기 때문이다.
KL divergence 는 암묵적으로 p(z) 가 평균 0 , 분산 1을 따를것이라고 가정하고 출발 하는듯 싶다.
(p(z) 가 평균 0, 분산 1을 따를 것이라고 가정하는 이유는, VAE 에서는 가능할듯 하다. 왜냐하면 그것에 맞춰서 Network 가 학습될것이기 때문이다.)
그랬을 때, 아래와 같이 Eq.2 와 같은 식이나온다. (가우시안을 따를 것이라고 가정 하기 떄문에 아래와 같이나오고

실제로 keras 도 아래와 같이 구현이 되어있다.
kld_loss = torch.mean(
-0.5 * torch.sum(1 + log_var - mu**2 - log_var.exp(), dim=1), dim=0
)
다시 돌아가서 VAE 로 돌아가서 하나의 설명을 덧붙이자면
Eq 3 과 같은 Reparametrization trick 을 사용하는데, 그 이유는
1. 단순히 z 를 Noise 없이 분포 시키면, 똑 같은 모델만 Recon 하게 된다.
2. Noise 를 가정하면 부드러운 latent space 분포가 만들어진다. 결국 우리가 하려는 것의 목적은 좋은 Latent space 를 만들고 그곳으로부터 sampling 하여 좋은 sample 를 얻고자 하는 목적에 부합하다.
3. 2에서 부드럽다 라는 말이 참 애매한데, 어찌보면 Overtuning 같은 것일 수도있고, 최근 Contrastive learning Yolo-R 과 같이 Represent learning 을 시도하려는 쪽에서는 이러한 Reparametrization Trick 을 이용해서 우리가 잘 알지못하는 잠재공간의 무엇인가를 모델이 알아서 학습 시키게 하려는 그런 시도라고 생각한다.

2-2. β- VAE
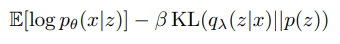
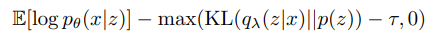
위에 나온 Loss 에 β 가중치를 곱한다.
β<1 로 만들면 모델이 Reconstruct 에 집중 할수 있도록 한다.
EQ 4-2 같은 경우에는 KL divergence 의 타우라고 하는 Treshold 값을 주었는데, 이 값을 줌으로써,
모델은 KL 다이버전스가 충분히 낮다(인코딩이 원하는 분포 대로 되었다) 일 경우에 전체적으로 loss 에 집중하고
KL 이 높을 때는 뒤에 term 이 상대적으로 커지게 되어서 무시하려고한다.
이러한 작업은 모델로부터 더 필요한것에 집중할 수 있도록 추가적인 정보(예산)를 주는 것이라고 해석하였다.
2-3. latent space manipulation
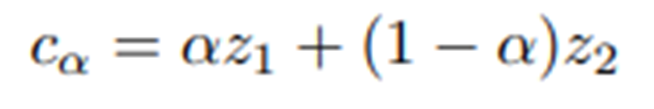
AE 의 목적은 compact 한 Representation 을 학습하는 것이고,
그렇다는것은 data 에서 small Perturbation 이 결과적으로 Recon 된 이미지에서 비슷해야한다.
그래서 sampling 된 z1,z2 사이에 무수히많은 C_a 를 interpolation 하고, 그것들은 다시 recon 했을 때 모두 Realistic 해야한다.
특히 z 는 가우시안 분포를 따를것이라고 가정했기 때문에, Spherical interporlation (구면을 따라) 하게 된다.
이러한 생성에 대한 실험은 Attribute vectors ( 음악의 속성 vector ) 를만들어서 추가 실험을 해보았다.논문내의 (5-5)
2-4. Recurrent VAEs
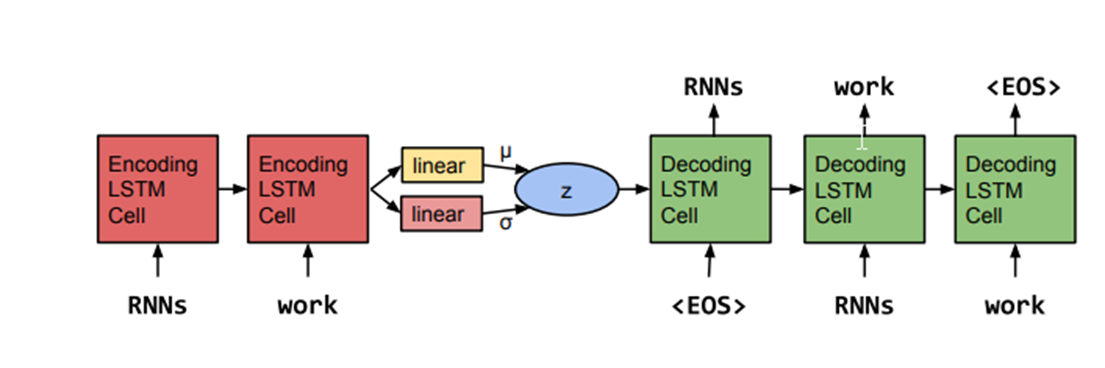
Recurrent VAE 모델을 위 fig 가 삽입된 논문을 refer 한다. (Generating Sentences from a Continuous Space)
특징 1. Encoder 의 LSTM output 중 hidden shell output h_T 를 이용해서 시그마,뮤를 예측한다.
2.Decorder RNN 에서는 잠재벡터 z 를 초기 shell 에서 initial state 로 입력 받고, decoding 한다.
3. 모델은 recon 과 동시에, KL Divergence 를 줄이는 쪽으로 계산된다.
하지만 2개의 한계점이 있다.
1. decorder 자체가 그럴싸하게 recon 은 잘하는데, z latent code 를 무시하는 경향이 있다. z 의 영향이 작아지면 KL도 작아지고 결국 autoencoder 로 서 역할을 못하게된다(?)
2. 모델이 긴 Seq 를 하나의 z space 로 Encoding 하게되므로 한계가 있다.
3. Model
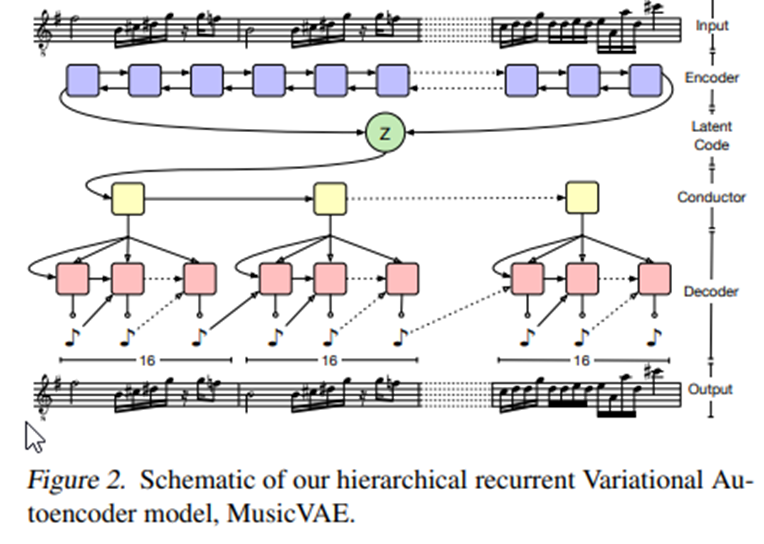
그래서 모델은 크게 3개의 part 로 구성되어있다.
Encoder, Conductor, Decorder
input data sequence = [x1,x2....xU]
Encoder : 2 layer LSTM 구조이고, 위 Refer 한 논문 과 같이 h_t 를 이용하여 latent code 인 z 를 생성한다.
(decoder) Conductor : Two layer undirectional LSTM 구조이고, 미리 구간 별로 나눠놓은 data sequence 에 대해서 매칭되도록 [c1,c2....cU] 를 generate한다.
Decoder : 2layer lstm 구조이고, 위의 출력인 c1...cu 를 decoder 의 output 과 concat 하여 input 으로 놓고 , initial state 는 모두 z 로 setting 한다. (특이한부분?)
Decorder 에서 이러한 조작을 한이유는 1.latent z 가 RNN 의 뒤로갈수록 limit 가 있었고 CNN 이면 그런 Receptive field 를 쉽게 줄일 수 있으나, RNN 의 경우에는 이게 제한이 없어서 어렵다고 설명하고 있다. 그래서 Decoder 의 ouput sequence 가 들어가는 영향을(concat,initstate)통해서 줄였다고한다.
decoder 의 state 을 conductor 의 state 로 전달 한경우에도 실험이 더 안좋아졌다고한다. Conductor 는 그래서 혼자서 잠재공간을 decoding 하는 역할에만 집중 하게 시켰다고한다.
*Multi sound 의 분리를 위해서 Melody, drum, bass 가 섞이는 경우 othgonal dimension 을 분리하였다고한다.
4. 결과
4-1 dataset
input : wav(midi) files
2bar , 16 bar 음악에서 마디에 해당되는 듯 싶다.
2bar = 2마디 = 2U = 32T , (1마디에 16개 구간이 존재한다로해석)
16bar = 16마디 = 16U = 256T , (1마디에 16개 구간이 존재한다로해석)
output seq : 마디당 16개의 quantized 된 note 를 16개의 인터발안에서 구분지어놓은 것 같다
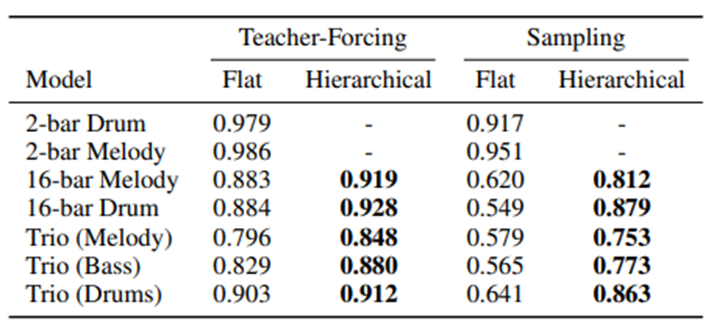
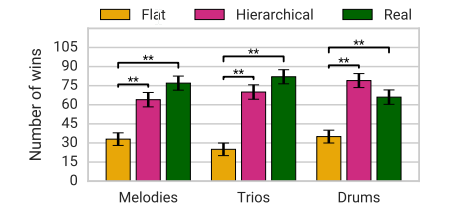
결과1. Flat 은 seq 를 한번에 넣은경우 Hierachical 은 아까와 같이 subsequence 로 놓은경우
Teacher forcing 은 GT 를 다음 output 의 input 으로 넣어 학습한경우 sampling 의 경우에는 predicted label 을 input 로 넣은경우 이다. 전체적으로 Hierachical-teacher-forcing 의 경우 더 좋은 결과가나온다.
결과 2. Interporlation 에 대한 결과이다.
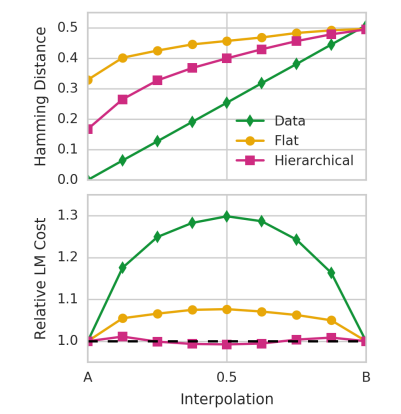
X 는 A,B 로 균일하게 interporlation 한 결과이고, (z 에서 했다고한다.)
결과적으로 나온 y 축의 결과는 propotion of timestep predictions that differ between the interpolation and seq A (시작점)
이라고한다.
아래는 마찬가지로 Language model cost 라고 하는데, 이게 뭔지..
결과 3
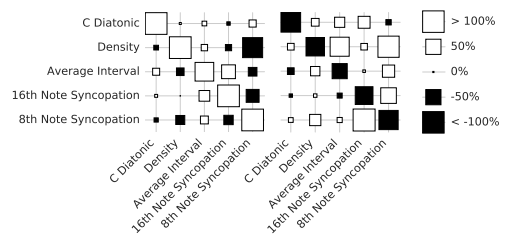
latent space 에서 음원에 특징의 방향을 만들어서 그것을 넣고(좌측), 뺏다는(우측) 실험이였다.
음원특징을 latent vector 로 만든것도 재미있고 각각 그 방향으로 벡터를 넣고 뺐을 때, 해당되는 특성이 얼마나 measure 되는지를 측정했다고한다. 이런시도들 이 너무 재밌고 신기하다고 생각한다.
결과 4 Listening test
얼마나 진짜 같은지 test 했는데 크게 차이나지 않은것 같다.