두번째 실험으로 Blackjack game 에 대해서 Reinforcement Learning 을 이용하여 최적의 답(hit or stand) 을 구해보는 인공지능을 만들어보도록 하겠다.
5장의 MonteCarlo method 와 4장의 Dynamic Programming 에 대해서
아래와 같은 의사코드를 바탕으로 모두 혼자서 구현하였고
github.com/Sangil55/ReinforceLearning_ex 여기에 코드를 첨부하였다.


몬테카를로부터 요약을 먼저해보자면
1.Episode 제작과정
MC 는 게임을 시뮬레이션한 것을 바탕으로 S A > R S A > R S A 이런 Episode 를 얻을 수 있었다.
그렇기 때문에 구현이 직관적으로 이루어질 수 있었다.
일단 episode 를 Generate 하는 것인데, 우리가 정책 pi 를 들고있다고 가정하면
Random 한 card 를 뽑는 과정을 통하여 쉽게 generate 할 수 있다.
2. Episode 진행 과정중 bust 가 나지 않는 상태과정에 대해서는 Reward를 조금 씩 주었다.
그이유는 21에 가까워졌다는 것으로 좋은 쪽으로 상태 이전이 일어났기에 일종에 Reward 를 부여한 것이다.
물론 Q(s,a) 가 그 값을 고려하여 update 하겠 지만, Q로인한 정책이 너무 소극적으로 바뀌게 되어 조금 더 직접적인 rewad도 필요했다.
3.간단한 게임이였지만 Ace 의 존재 (1 or 10) 떄문에 상태전이가 복잡한 경우가 생기더라,
다만 MC 의 장점이기도했지만, Episode 를 만들때만 주의하게 되면 , 그러한 상태 전이를 뒤에서 고려할 필요가 없었다.
4.구현에 유리함이 있었지만 상대적으로 많은 Episode (3만번)를 generate 하고, 그 것으로 Q값을 Q*값으로 수렴 시키고 최적 정책 pi 를 구했지만, 그마저도 data 불균형이 생기게 되더라, 그말인 즉슨, 자주오게 되는 state 에 대해서 update 가 자주일어나지고, 반대인 적은 case 도 생기게 되어, 적은 case 에 대해서 값이 들죽날죽해진다.
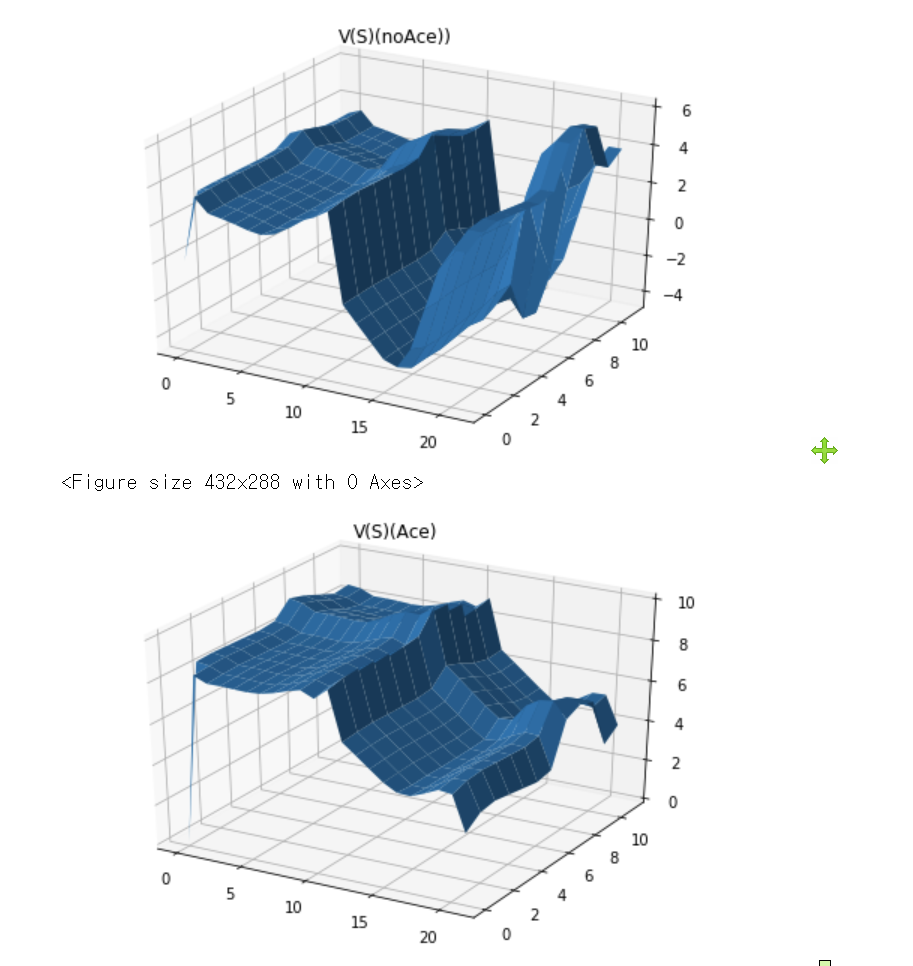
MC 결과를 지켜보자
ace 가 없는 경우 Q(S,0=stand) 의값, ace 가 없는 경우 Q(S,1=hit) 의값,
x 축은 내 카드합(0~20) y 축은 딜러 카드의 숫자이다.

ace 가 있는 경우 Q(S,0=stand) 의값, ace 가 있는 경우 Q(S,1=hit) 의값,
x 축은 내 카드합(0~20) y 축은 딜러 카드의 숫자이다.

Q값이 날카롭고 울퉁불퉁 하다 = 충분히 수렴시키지 못하였다.
사실 노트북으로 에피소드를 30000번 돌린 회수이긴한데,
ACE 를포함 한경우라면 3000번도 안돌아갔을거다.
그와중에 합이 13~20, 으로 분산이 된다치면 .. state 개수에 비해서 시행회수가 아직 너무 작다.
어찌됫건 ace 가있는경우 Q(S,1) 값이 ace 없는 경우 Q(S,1) 보다 대체적으로 높게나온것을 볼수 있다.
최적 정책은(Ace 없는경우)

ace 가 있는경우

ace 가 있는경우 최적정책이 더 1로(hit) 으로 덮여야 하는데, 듬성듬성 덮여있다.
전체적으로 dealer 패가 높을수록 더 공격적으로 하라고 지시한듯 하다.
역시 충분히 더돌려보고싶으나 수렴이 제대로 되고있는지 모니터링 하기가 꽤 까다롭다.
이번강화학습을 구현하면서 느꼈지만, 비교적 적은 state 의 예제를 구현해보는 데도, 구현하기에 꽤 까다롭고,
debuging과 Q 값, 정책값등을 같이 모니터링 하면서 코드를 지속적으로 수정 해주어야 한다.
하지만 예제코드를 구현하면서 어떻게 돌아가는지 체험해본 것 같다.
다음으로 DP 로 구현 과정을 요약하자면
1. 상태전이 확률 설정은 카드값이 나올 확률로 대체 한다.
2. Dealer 의 첫 숫자 - (17~21) 의 최종 기대값도 미리 계산된 페이지를 참고한다.
www.blackjackinfo.com/dealer-outcome-probabilities/
3. Dealer 의 숫자 = 기댓값로 생각하여 승패를 예측한다.
4. Ace 가 있을 경우 17>7 로 가는 등의 상태전이 확률이 필요하다.
5. Q 대신 V 를 사용하며 수행 후 계산된 가치함수인 V의 결과는 아래와 같다.
결과를 요약해보자면, 상대적으로 MC method 에 비해 완만하다. 확률적으로 승률을 계산했기 떄문에
당연한 결과이고, 사실 수렴을 마쳤다고 봐도된다.
또한 적은 회수의 반복만으로도, V, pi 가 수렴을 한 것을 볼 수 있었는데
정책은 아래와 같다.

ace 가 있을 경우 18 까지 hit 을 하라는 결론~ 과 그렇지 안흘경우 13까지 hit을 하고, 14부터는 stand 를 하되,
Dealer 의 카드가 6~8인 경우 좀더 공격적으로 하라는 결론이였다.
결과적으로 MC method 는 아직 수렴중인 듯하며, 사실 정확한 Q와 pi 를 얻자면 더많은 시행 착오를 겪어야 될 듯하다.
원래 이예제를 풀게 된의도는
MC vs DP 였다.
결론적으로 DP 를 구현할 수 만 있다면 DP 를 구현하는게 몇배는 더좋은 알고리즘을 만들어낸다.
즉, 상태전이확률과 승률의 기대값을 높은 신뢰도로 이미 알고 있다면,
굳이 많은 에피소드의 학습 없이도 답과 유사하게 만들어 낼수 있다. 일종의 Generative model 과도 일맥 상통한다고 보면된다.
하지만 실제 우리환경에서 이 것을 정확히 알지 못하는 대부분의 경우 에 있어서는 MC 로 구현 할 수 밖에 없을 것이다.
'Machine.Learning > reinforcement' 카테고리의 다른 글
| Future of Reinforcement learning (0) | 2021.01.06 |
|---|---|
| Cliff exploration, Sarsa vs Q-Learning (0) | 2020.12.06 |
| 6장 TD (0) | 2020.11.30 |
| 5. Monte Carlo method (MC method) (0) | 2020.11.30 |
| 4. 4장 DP (Policy Evaluation and improvement) (0) | 2020.11.30 |